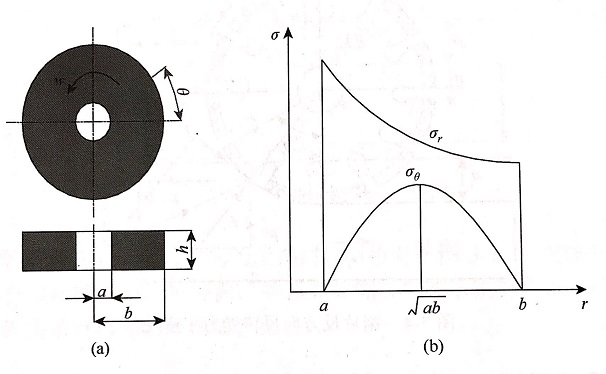
在混凝土鋸片尚未接觸到材料的過程中,可將鋸片視為內外半徑分別為a、b,厚度為h(簡化為厚度是同一個厚度且厚度遠小于半徑)的空心圓盤,如圖3-5所示,內孔表面為自由邊界。
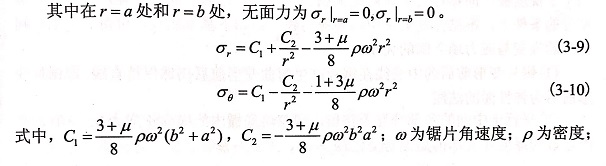

在彈性力學中,應力和應變是一一對應的關系,因為混凝土鋸片的直徑與鋸片厚度的比值遠大于100,且鋸片的軸向變形與厚度的比值很小(遠小于0.2)。
所以混凝土鋸片屬于小撓度板,而鋸片的彎曲問題又屬于三維問題,為了簡化計算,在滿足求解精度的條件下,根據彈性力學中的薄板問題。
做如下基本假設,可得到鋸片的應變與應力場之間的關系。
(1)鋸片變形前后的中法線在鋸片產生彎曲變形前后仍然保持直線,即鋸片變形前后為彈性面的法線。
(2)平行于中面的各部分互不擠壓,即忽略薄板內的橫向正應力(σz=0),并假定板的厚度在變形前后沒有變化(εz=0)。
(3)鋸片在彎曲前后其中面始終保持在中性位置,鋸片中性面上的各點沒有平行于中面的位移和應變,即在z=0上,u=v=0(u、v分別為x、y方向上的位移分量。
