金剛石鋸片模態實驗中傳遞函數的確定:
對于N自由度的振動系統,假設該阻尼成比例性,在這種簡化情況下,多數是符合實際要求的,對式(2-1)兩邊進行拉普拉斯變換,且假定{x(O)}=0和{x(O)}=0,可得

式(2-4)中的adt(s)稱作振動系統的特征方程,是Z(s)的行列式。傳遞函數矩陣可通過線性代數計算的方法改寫為

若s=jω,應用拉普拉斯變換轉化為傅里葉變換,通過傳遞函數矩陣變換成頻響函數矩陣,基于定理得到振動系統在頻域內輸出和輸入的關系可表示為
χ(ω) = H(ω)F(ω) (2-10)
基于振型矩陣的加權正交條件,假定振型矩陣C可由阻尼矩陣[Φr]對角化則動態矩陣可表示為

基于模態參數表示的頻率響應函數:

公式(2-14)可以概述為j點單獨激振時,i點測得響應函數Χi(t)與激振力fj(t)的傅里葉比值。由于一般來說Z(S)是對稱矩陣,所以H(ω)稱為矩陣,因此可以得出以下關系式:
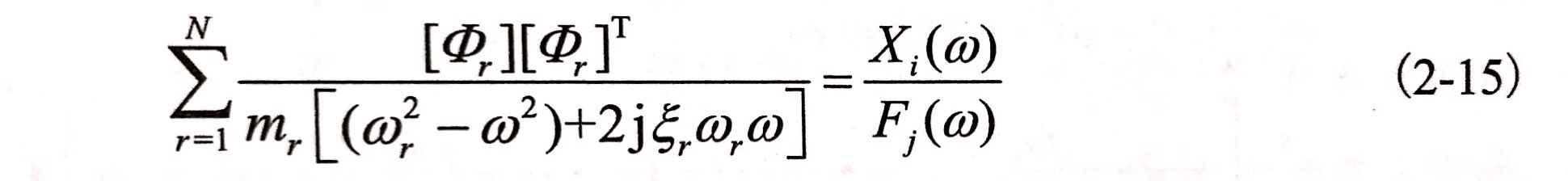
頻響函數的互易性是檢驗頻響測試精度的一項重要指標,由此說明測得頻響函數某一矩陣的一行或是一列就可確定結構的全部模態函數。
這就是金剛石鋸片模態實驗傳遞函數的確定方法。
