昌利在判斷金剛石鋸片結構的動態特性是通過模態參數直接體現出來的

  昌利在判斷金剛石鋸片結構的動態特性是通過模態參數直接體現出來的，很業內模態參數應用到機械結構的動態分析中。通常來說，頻域法和時域法是識別模態參數的兩類基本方法。

  頻域法是一種應用實際測量的頻響函數識別系統模態參數的方法。具體操作方法是在結構選定一點為激勵點，通過電荷放大器測量激勵點與響應點間的時域信號。

  通過動態測試分析軟件運算將時域信號轉換成頻域信號，將此信號通過整合得出響應的頻響函數，最后通過數據識別系統得到模態參數。

  此方法由于操作簡單、識別精度高、有效地去除金剛石鋸片噪聲影響的特點，通常應用于阻尼較大、結構復雜的系統中。

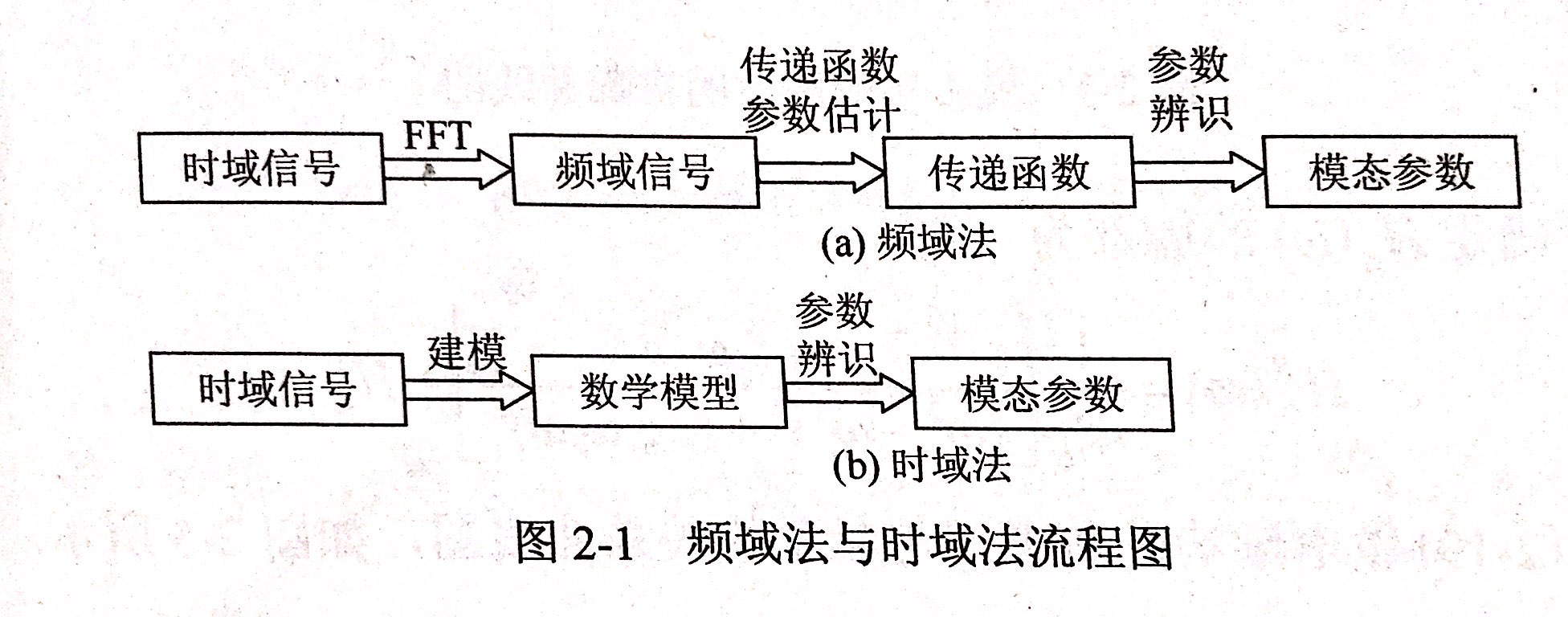
  時域法與頻域法的差別是直接在時域中識別，不用把信號變換到頻域中去。通常應用于故障檢測。其流程圖如圖2-1所示。

  對于N自由度振動系統，由于式(2-13)參考：金剛石鋸片模態實驗原理-傳遞函數的確定，則在j點激振、i點響應的實模態頻響函數為

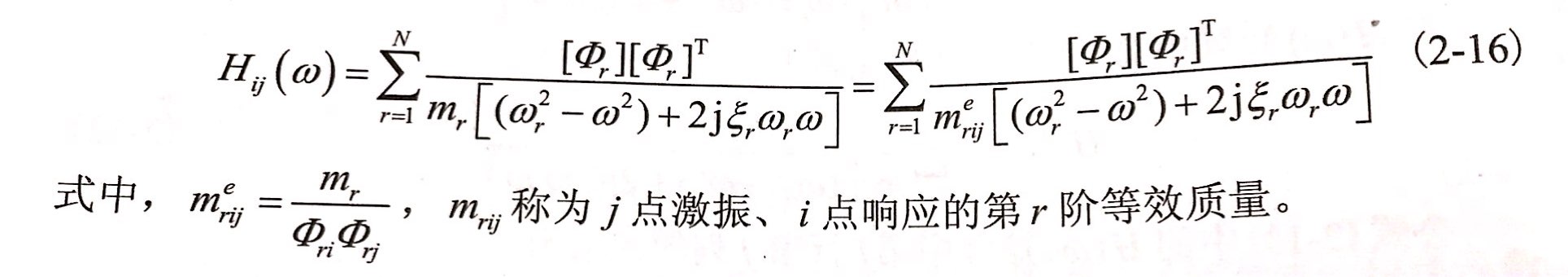
  如果ω接近振動系統某一階模態的固有頻率，則該階模態起主導作用，即主模態。

  主模態對激勵頻率起主要作用，而其他模態相對于主模態而言，所產生的影響偏小。

  當其余各階模態距離主模態較遠時，它們頻響函數的影響就會較小，其曲線沒有較大波動，一般用復數H_c來表示。其中公式(2-16)可近似為

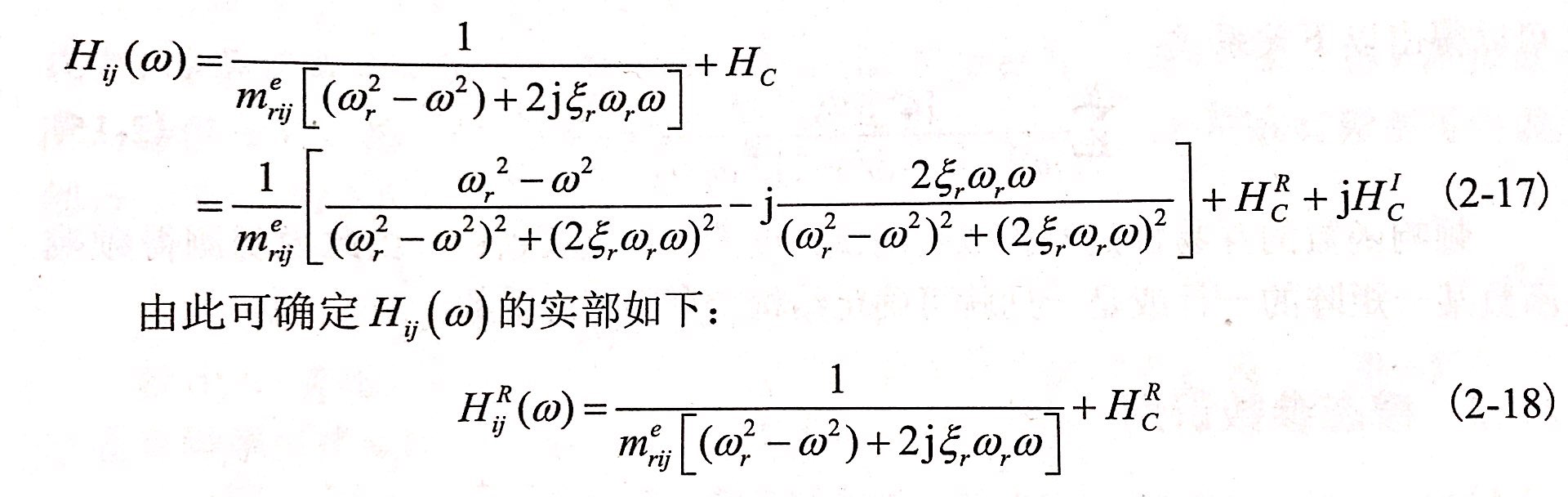
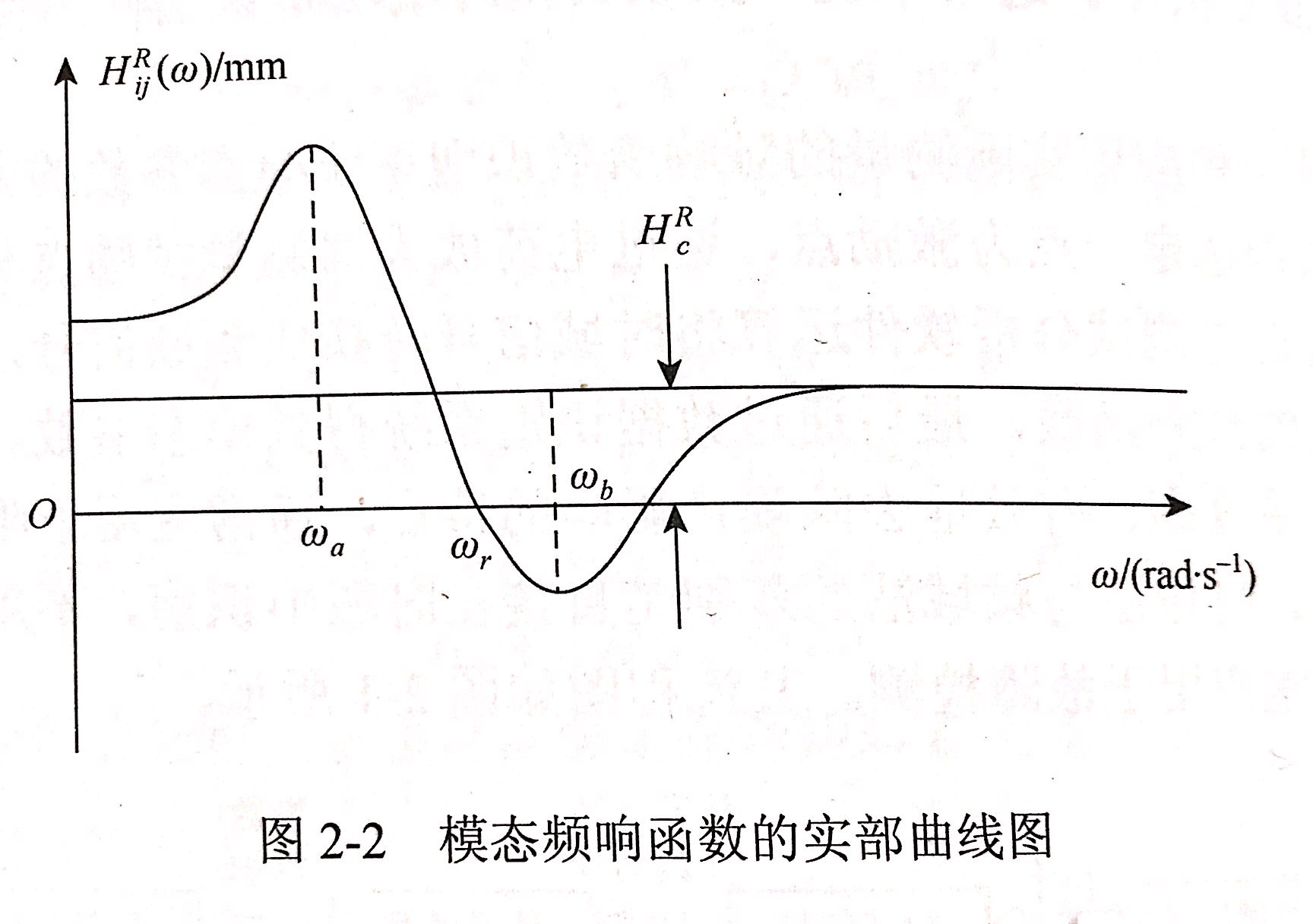
  根據式(2-18)可以做出頻響函數實部與頻率的關系曲線圖，如圖2-2所示。

  由此可確定H_ij(ω)的虛部為

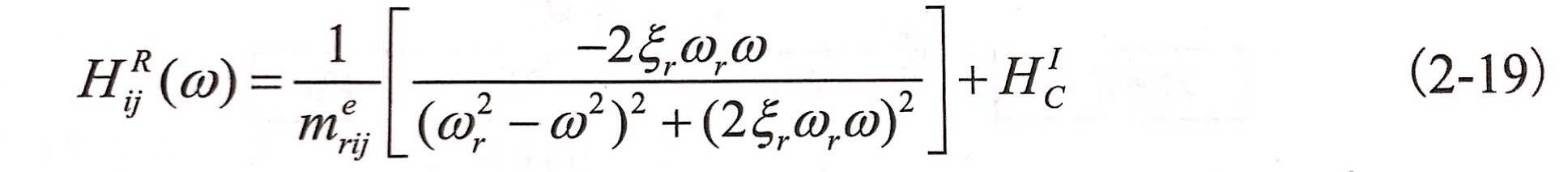
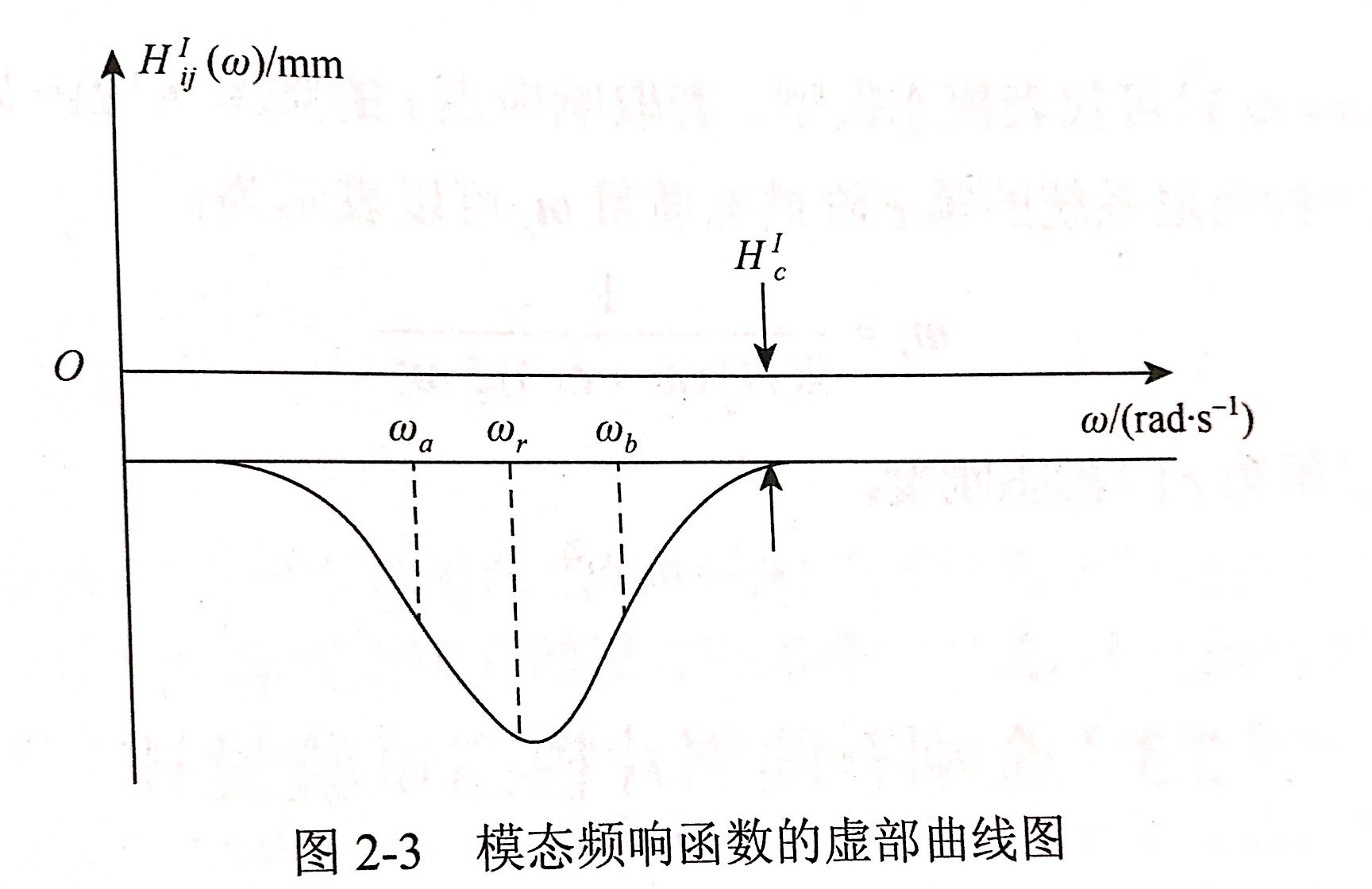
  根據式(2-19)做出頻響函數虛部與頻率的關系曲線圖，如圖2-3所示。

  通過圖2-2和圖2-3顯示的兩條曲線，就可以確定模態參數，具體步驟如下：

  第一步是固有頻率的確定。由圖2-2可以看出，固有頻率ωr為實譜曲線和直線H^R_tj(ω)=H^R_C的交點。一般來說，多自由度系統的剩余模態H^R_C對固有頻率的影響難以確定，且固有頻率隨HRC的變化而變化。

  為避免以上問題，可通過圖2-3來確定固有頻率。在使用此方法確定固有頻率時，且ω=ω_r與圖2-3所示曲線的峰值相對應。由圖2-3可以看出，波峰值明顯，有利于頻率的確定;

  第二步是阻尼比的確定。在公式(2-13)中，對ω求導后求解，可得兩個極值分別為

  由以上兩個極值，可得出其阻尼比系數為

  第三步是振型和模態參數的確定，對于主模態，由式(2-19)可得，當0=O時，有

  因此[Φ_r]=[ H^R_tj(ω=ω_r)] 可代表模態振型。若取響應點的頻率響應函數，且對響應點歸一化，則結構阻尼系統的第r階模態質量m_r可以表示為

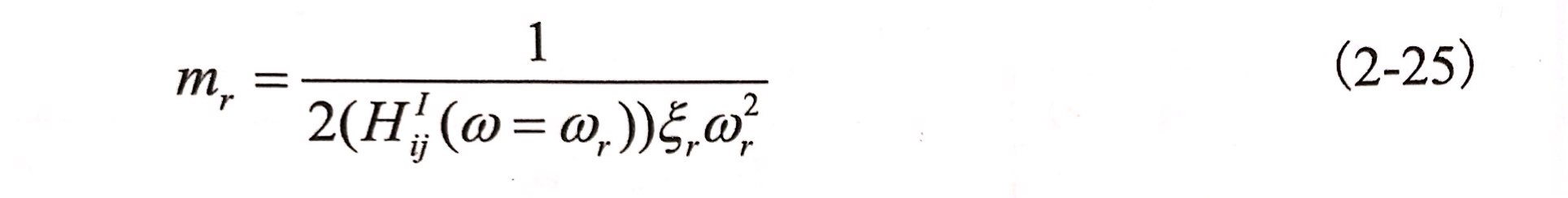
  因此可以得第r階模態剛度：k_r=m_rω²_r     (2-26)

  這就是金剛石鋸片模態實驗中模態參數的識別方法。