蒙特卡羅 (Monte-Carlo) 方法又稱隨機抽樣技巧或統計試驗方法,適用于金剛石鋸片的可靠性方面問題的檢測。
Monte-Carl法是與普通數值計算方法相差很大的一種計算方法,統計方法是它的主要依據,將所求解的問題的概率模型相聯系比較逼真地描述事物的特征及物理試驗程。
借助計算機技術進行模擬統計和抽樣調查從而獲得比較準確的計算結果,而且能夠完成一些數值計算難以解決的問題,因此蒙特卡羅法的應用范圍越來越廣。
蒙特卡羅法在解決金剛石鋸片可靠性問題方面的優點:
① 能夠比較逼真地描述具有隨機性質的事物的特點及物理過程,直觀易見;
② 受幾何條件限制小,計算精度高;
③ 收斂速度與問題的維數無關,通用性強;
④ 問題的非線性和極限狀態曲面的復雜性無須考慮,有效地避免了數學求解難度;
⑤ 該方法可同時計算出多個未知量和多套方案;
⑥ 擁有計算誤差易于確定、程序結構較為簡單。
同樣,蒙特卡法也有自身的缺點,首先是計算量比較大,使其不能應用于大型機構可靠性計中;收斂速度較慢;誤差具有概率性等。
為了降低計算的復雜程度,減少所需樣本數量,實際應用中多采用減少樣本方差、提高所選樣本的質量等多種方法。因此 , 在蒙特卡羅法基礎上產生了多種抽樣法,如近似-修正抽樣法、 指數分布抽樣法、多維分布抽樣法等。
蒙特卡羅法其基本思想是確定包含某一隨機變量且與所研究問題相對應的隨機模型,使該模型的一個或者多個數字變量 (如數學期望等) 剛好為它得到問題解,接著運用足夠多的隨機試驗得到大批的隨機抽樣值,最終利用抽樣值計算得數學期望的估計值。
在該理論基礎上,將機構功能函數定義為 Z=g(X1,X2,...,Xn) 式中X1 為任意分布的隨機變量。對 Xi(i=1,2,...,N) 進行N次隨機抽樣,得到Xij(j=1,2,...N)。 將第j 組 Xij值代入功能函數, 得到Zj (j=1,2,...N)值。設在N個Zj <0,則機構的隨機概率可以描述為
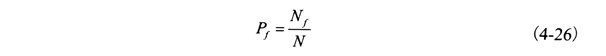
由式(4-26)可知,機構的失效概率為大批隨機抽樣中獲得的失效概率與總隨機抽樣次數的比值。該結論也是蒙特卡羅法的核心觀點。因此利用蒙特卡羅法計算機構的失效概率時,需要進行大批的金剛石鋸片隨機試驗,確保抽樣次數,抽樣次數多,則機構失效概率的計算結果越精確。一般采取 95%的置信度保證 Monte-Carl法的計算精度,其允許誤差ε為

蒙特卡羅(Monte-Carlo)法的一般步驟為:
① 由實際問題抽象數學模型;
② 匆依據所抽數學模型的特點, 進行對應的概率分布的多次重復抽樣;
③ 將抽樣模擬結果行統計處理;
④ 得出結論。
蒙特卡羅(Monte-Carlo)法所特有的優點, 使得它的應用范圍越來廣。它不僅在金剛石鋸片可靠性分析、統計物理、真空技術、數學問題方面應用廣泛,現在也大量應用工程上。
