對于金剛石鋸片的BP神經網絡,有一點是非常重要的。即對于任何的一個連續函數在其區間內都可以通過單隱層BP 網絡逼近,而如果對于一個不連續的函數,則需兩個隱含層用以形成輸入信號轉換和處理信號,其能力隨著層數的增加而增加在有足夠多的隱含層節點的情況下,輸入模式總能轉換為適當的輸出模式。
但如果隱含層層數過多就會造成神經網絡過于復雜,從而帶來誤差反向傳播的計算程越復雜,從而訓練時間增多,并且隱含層的增加還可能會使網絡的權重難整到最小誤差處。因此,本設計采用一個隱含層。
一般來說 , 確定隱含層神經元的數目需要根據神經網絡設計者的經驗和很多次試驗來確定,因而不存在一個理想的解析式表示。因為隱含層神經元個數與測問題的要求,輸入輸出單元的數目有直接關系,隱含層神經元數過多會導致習時間過長、誤差值不確定最佳,同時導致容錯性差、無法識別之前沒看到的樣本。
一般來說, 可用經驗公式n1 =(根號n+m)+a 來選擇最佳隱含層神經單元數,其中,m 是輸出神經元數, n 是輸入單元數, a是[1,10]的常數。本書中 n=3, ,m=3, 取a分別為 1、 2、 3、 4, 因此隱含層神經元個數可以在 3~6 進行嘗試。設置不同隱含層神經元個數, 預設誤差精度 0.1, 分別經過網絡訓練。訓練結束所得金剛石鋸片神經網絡法隱含神經元個數與誤差的關系如圖 8-27和圖 8-30 所示。
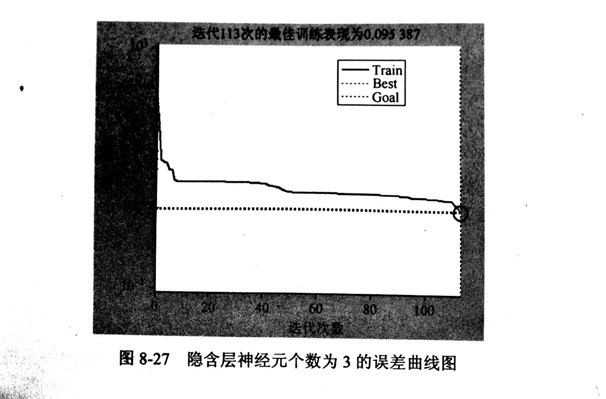
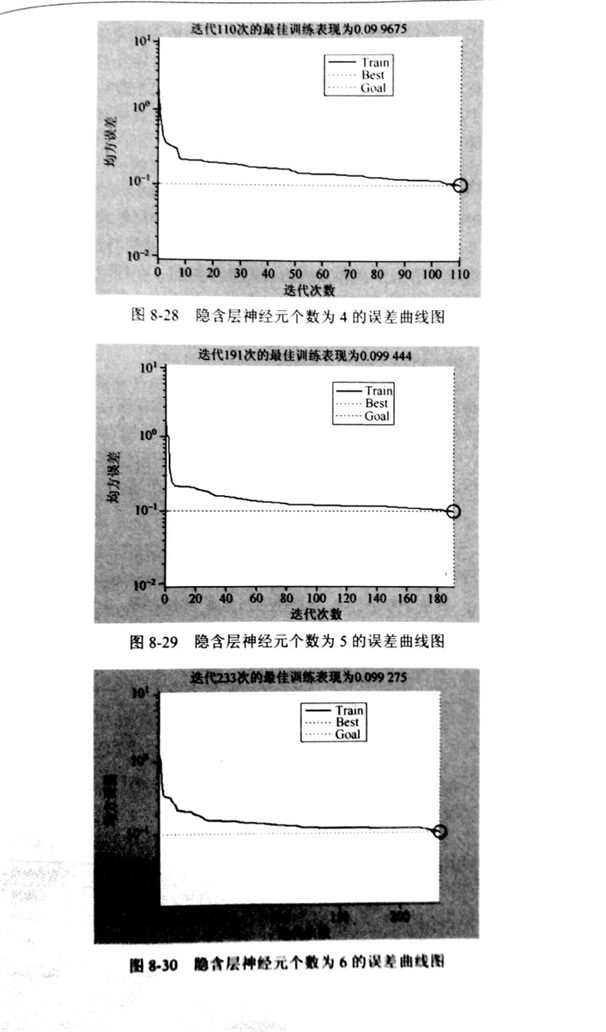
從圖 8-27和圖 8-30 中可以看出 , 金剛石鋸片神經網絡法隱含層神經元個數應適當選擇, 隱含層神元數過多會導致學習吋間過長、誤差值不確定最佳,同時導致容錯性差、無法識別之前沒看到的樣本。
綜合上圖,網絡結構隱含層神經元個數與誤差關系來當隱含層神經元個數為 4 時, 訓練次數為 110 次時其誤差就相對穩定了, 網絡逼近效果最好。 因此金剛石鋸片神經網絡法隱含層神經元的個數定為5。
